本文最后更新于 2024-07-13T22:38:59+08:00
中点画线是比较基础的画线法,重点是确定递推公式。
中点画线法
基本推导
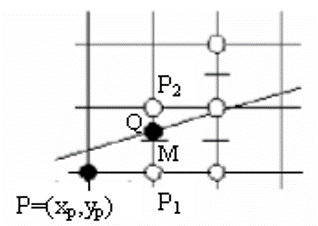
假设直线的斜率在0、1之间,假设x坐标为 xp 的各像素点中,与直线最近者已经确定为 P(xp,yp) 。那么,下一个与直线最近的像素只能是正右方的 P1(xp+1,yp),或者右上方的 P2(xp+1,yp+1) 两者其中之一。
令 M 为 P1 和 P2 的中点,易知 M 的坐标为 (xp+1,yp+0.5) 。
设 Q 为理想直线与垂直线 x=xp+1 的交点。
显然,若 M 在 Q 的下方,则 P2 离直线更近,应该作为下一个像素;否则就应该取 P1 。
假设直线的起点和终点分别是 (x0,y0) 和 (x1,y1) 。则直线方程为:
F(x,y)=ax+by+c=0
其中
a=y0−y1
b=x1−x0
c=x0y1−x1y0
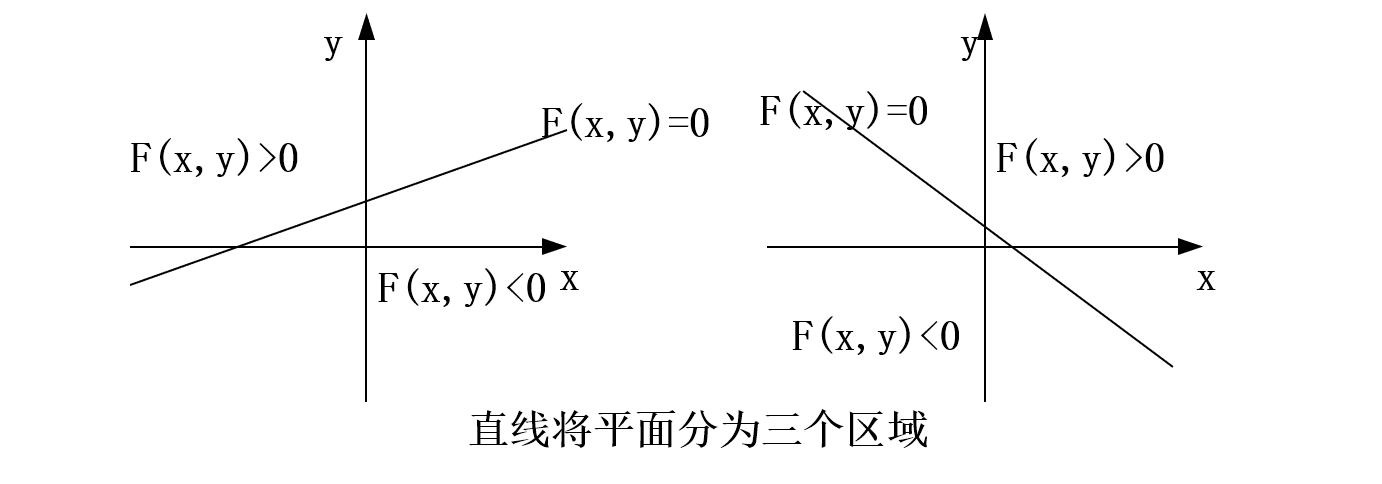
该直线方程将平面分为三个区域:
对于直线上的点,F(x,y)=0 ;
对于直线上方的点,F(x,y)>0;
对于直线下方的点,F(x,y)<0。
此时我们将 M 点带进直线方程,通过判断代入方程的结果的正负,即可判断 M 点是在直线方程上方还是下方。
即判别式 d=F(M)=F(xp+1,yp+0.5)=a(xp+1)+b(yp+0.5)+c
此时,我们就有了对 y 的更新方法
y={y+1yd<0d≥0
当 d<0 时,说明 M 点在直线的下方,那么直线离 P2(xp+1,yp+1) 点更近,所以下一个逼近于直线的点应该取 P2(xp+1,yp+1),即 y=y+1 ,反之,当 d>0 时,说明 M 点在直线的上方,那么直线离 P1(xp+1,yp) 点更近,所以下一个逼近于直线的点应该取 P1 ,即 y 不变。当 d=0 时说明 M 点在直线上,那么取 P1(xp+1,yp) 或 P2(xp+1,yp+1) 皆可。由于假设 ∣k∣<1 ,所以 x 每次都增加 1。
递推误差项d
因为我们求d的时候用了乘法以及浮点数,所以对于计算机而言,硬件开销大,为此我们要想办法找到递归的方法来求d。
当 d≥0时:
由上面的结论我们知道,此时我们取的点是P1(xp+1,yp),而我们要画的下一个点为P3(xp+2,yp),或者P4(xp+2,yp+1)。将P3(xp+2,yp)与P4(xp+2,yp+1)的中点M(xp+2,yp+0.5)带入直线方程(x,y)=ax+by+c=0中可以得到
d1=F(xp+2,yp+0.5)=a(xp+2)+b(yp+0.5)+c=a(xp+1)+b(yp+0.5)+c+a=d+a
此时,d的增量为a。
当d<0时:
由上面的结论我们知道,此时我们取的点是P2(xp+1,yp+1),而我们要画的下一个点为P4(xp+2,yp+1),或者P5(xp+2,yp+2)。将P4(xp+2,yp+1)与P5(xp+2,yp+2)的中点M(xp+2,yp+1.5)带入直线方程(x,y)=ax+by+c=0中可以得到
d1=F(xp+2,yp+1.5)=a(xp+2)+b(yp+1.5)+c=a(xp+1)+b(yp+0.5)+c+a+b=d+a+b
此时,d的增量为a+b。
至此,我们对d的递推关系便找到了
dn={dn−1+a+bdn−1+ad<0d≥0
中点画线算法公式
现在我们可以找到当∣k∣<1时的中点画线算法了
(1) 输入直线的起始和终止端点 P0(x0,y0)和 P1(x1,y1);
(2) 计算初始值a=y0−y1,b=x1−x0,c=x0y1−x1y0,d=a+0.5∗b,x=x0,y=y0
(3) 绘制点(x,y);
(4) 判断 d 的符号。若d<0,则(x,y)更新为(x+1,y+1),d 更新为 d+a+b;否则(x,y)更新为(x+1,y),d 更新为 d+a;
(5) 当直线没有绘制完成时,跳转到步骤(3)执行,否则算法结束。
优化中点画线算法
对于上面的算法,在步骤(2)中有浮点运算,不利于硬件实现,因此我们需要对之进行改进。由于 d 只是用来判断正负用的,因此我们用 2d 来代替 d 并不会影响算法的执行结
果。用 2d 代替 d 的新算法如下所示:
(1) 输入直线的起始和终止端点 P0(x0,y0)和 P1(x1,y1);
(2) 计算初始值a=y0−y1,b=x1−x0,c=x0y1−x1y0,d=2∗a+b,x=x0,y=y0,d1=2∗a,d2=2∗(a+b);
(3) 绘制点(x,y);
(4) 判断 d 的符号。若d<0,则(x,y)更新为(x+1,y+1),d 更新为 d+d2;否则(x,y)更新为(x+1,y),d 更新为 d+d1;
(5) 当直线没有绘制完成时,跳转到步骤(3)执行,否则算法结束。
总结
通过上面的分析可知,中点画线算法的基本思想就是借助一个决策变量 d 的正负符号,
来确定下一个该点亮的像素点。中点画线算法有很多优点,如下所示。
(1) 不必计算直线的斜率,因此不必除法运算;
(2) 不用浮点数,只用整数;
(3) 只有加法和乘 2 运算,在计算机内部用位移操作实现即可,因此效率很高。
正因为中点画线算法有上述优点,因此其运算速度很快,利于硬件实现。

